Integral adalah konsep matematika yang berhubungan dengan menghitung luas daerah di bawah kurva fungsi. Secara formal, integral adalah operasi matematika yang menghitung luas daerah di bawah kurva fungsi yang diberikan dalam suatu interval tertentu. Integral adalah operasi yang berlawanan dengan turunan.
Fungsi integral sangatlah penting dalam berbagai bidang, termasuk matematika, fisika, dan teknik. Dalam matematika, integral digunakan untuk menghitung luas daerah tertentu di bawah kurva fungsi. Dalam fisika, integral digunakan untuk menghitung besarnya kuantitas fisika seperti kecepatan, percepatan, dan energi. Dalam teknik, integral digunakan untuk menghitung berbagai parameter seperti kekuatan material, daya tahan material, dan berbagai parameter teknis lainnya.
Penerapan integral dalam kehidupan sehari-hari antara lain pada perhitungan luas bidang, volume benda, perhitungan integral dalam analisis matematika, dan sebagainya. Dengan menggunakan integral, banyak masalah matematika dan teknik yang sulit dapat dipecahkan dengan mudah dan akurat.
Integral sendiri diartikan sebagai objek matematika yang bisa didefinisikan sebagai area atau generalisasi. Integral berkaitan dengan turunan sebagai objek dasarnya. Lambang integral menyerupai huruf “S”. Hanya saja lekukan perutnya datar.
Selain itu, integral juga memiliki beberapa jenis yang berbeda, seperti integral tak tentu, integral tentu, integral ganda, dan integral lipat. Integral tak tentu adalah jenis integral yang digunakan untuk mencari fungsi asal dari suatu turunan. Integral tentu adalah jenis integral yang digunakan untuk menghitung luas daerah di bawah kurva fungsi pada interval tertentu. Integral ganda adalah jenis integral yang digunakan untuk menghitung volume benda tiga dimensi yang dibatasi oleh permukaan yang diberikan. Sedangkan integral lipat adalah jenis integral yang digunakan untuk menghitung volume benda yang berbentuk kompleks dalam ruang tiga dimensi.
Dalam penggunaannya, integral membutuhkan beberapa teknik dasar, seperti teknik substitusi, teknik integrasi parsial, dan teknik integrasi dengan pecahan parsial. Teknik-teknik ini berguna untuk menyelesaikan berbagai masalah integral yang kompleks.
Dalam penelitian dan pengembangan, integral juga sering digunakan dalam analisis data, khususnya dalam statistik. Integral digunakan untuk menghitung probabilitas dari suatu kejadian, dan juga untuk menghitung berbagai ukuran statistik seperti mean, median, dan standar deviasi.
Dalam kesimpulannya, integral adalah konsep matematika yang sangat penting dan memiliki banyak aplikasi di berbagai bidang ilmu pengetahuan dan teknologi. Dengan pemahaman yang baik tentang konsep dan teknik integral, kita dapat memecahkan berbagai masalah matematika dan teknik yang kompleks dengan lebih mudah dan akurat.
Integral Tak Tentu
Integral tak tentu (indefinite integral) adalah integral yang tidak memiliki batas-batas nilai tertentu sehingga hanya diperoleh fungsi umumnya saja disertai suatu konstanta C.
Setiap bentuk operasi matematis pasti memiliki operasi kebalikan atau invers, seperti penjumlahan dan pengurangan, perkalian dan pembagian, akar dan pangkat. Kebalikan itu juga berlaku pada turunan, di mana kebalikan dari turunan adalah integral.
Persamaan dasar integral tak tentu merupakan rumus umum untuk mengonversi fungsi turunan menjadi fungsi integral. Adapun persamaan dasarnya adalah sebagai berikut.
syarat n ≠ -1
Persamaan di atas menunjukkan bahwa proses integrasi menyebabkan kenaikan pangkat suatu fungsi, di mana fungsi awalnya berpangkat n dan fungsi integrasinya berpangkat n + 1.
- Sifat-Sifat Integral Tak Tentu
Sifat-sifat integral tak tentu adalah bentuk lain dari operasi integral sedemikian sehingga bisa memudahkanmu dalam menyelesaikan permasalahan terkait integral. Adapun sifat-sifat integral tak tentu adalah sebagai berikut.
-
- Sifat Pertama
Sifat pertama berkaitan dengan integral suatu fungsi yang memuat suatu konstanta seperti:
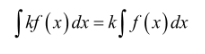
Jika kamu menjumpai bentuk seperti di atas, keluarkan saja konstanta k dari tanda integral, sehingga kamu bisa fokus menyelesaikan integral fungsinya.
-
- Sifat Kedua
Sifat kedua berlaku untuk penjumlahan dua fungsi di dalam integral seperti berikut.
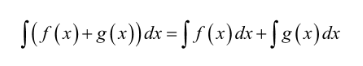
Dua fungsi yang dijumlahkan dalam satu tanda integral bisa kamu ubah menjadi penjumlahan integral masing-masing fungsinya. Sifat ini bisa memudahkanmu dalam menyelesaikan fungsi-fungsi yang cukup panjang. Misalnya:
-
- Sifat Ketiga
Sifat ketiga berlaku untuk pengurangan dua fungsi di dalam satu tanda integral. Konsepnya sama seperti penjumlahan dua fungsi.
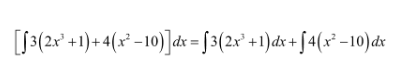
Ingat, pada pengurangan tidak berlaku sifat komutatif.
Lalu, bagaimana dengan perkalian dua fungsi integral? Pada perkalian dua fungsi, kamu harus mengalikan semua elemen fungsi tersebut satu persatu hingga dihasilkan bentuk penjumlahan. Misalnya, (x – 2)(x + 5) = x2 + 3x – 10.
Namun, khusus perkalian dan pembagian dua fungsi di dalam integral, akan kamu pelajari di bab
- Integral Tak Tentu Fungsi Trigonometri
Ternyata, tidak hanya fungsi aljabar yang bisa diintegralkan, tapi juga fungsi trigonometri. Adapun bentuk integral fungsi trigonometri adalah sebagai berikut.
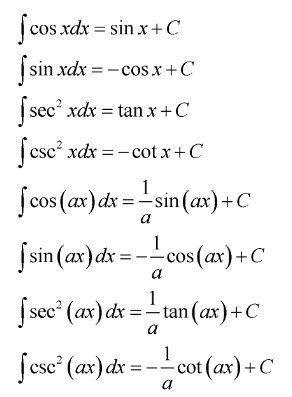
Jika kamu menjumpai soal-soal integral trigonometri, lakukan manipulasi fungsi sedemikian sehingga mengarah pada bentuk di atas.
Integral Substitusi
Integral Substitusi adalah metode penyelesaian masalah melalui integral dengan cara substitusi kepada bentuk yang lebih sederhana, bentuk sederhana yang dimaksud adalah berkaitan dengan turunan suatu variabel.
Merubah dari bentuk yang belum dikenal menjadi lebih mudah dikenal atau bentuk primitifnya.
Rumus umum dari integral substitusi yakni :

Untuk lebih memahami, perhatikanlah contoh soal integral substitusi dan pembahasannya berikut:


Demikianlah pembahasan mengenai Integral. Semoga bisa bermanfaat dan dapat digunakan bagi kamu yang sedang membutuhkan, terima kasih.







