Rumus Diskriminan – Rumus diskriminan adalah sebuah formula matematika yang digunakan untuk menghitung nilai diskriminan dari suatu persamaan kuadrat. Formula ini berguna untuk menentukan jumlah akar atau solusi dari persamaan kuadrat tersebut, apakah ada dua akar, satu akar ganda, atau tidak memiliki akar real.
Dalam matematika, diskriminan adalah suatu nilai yang menjadi penentu sifat-sifat dari akar suatu persamaan kuadrat. Dengan nilai ini, bisa menentukan apakah suatu bentuk persamaan kuadrat memiliki penyelesaian berupa akar real atau tidak.
Diskriminan juga memiliki pengertian hubungan antara koefisien dalam persamaan kuadrat untuk mencari akar persamaan dan ciri-ciri yang lainnya.
Secara umum, diskriminan adalah suatu nilai pada persamaan kuadrat yang membedakan banyaknya akar persamaan itu sendiri.
1. Rumus Diskriminan Persamaan Kuadrat
Kegunaan diskriminan adalah untuk menentukan jenis akar-akar persamaan kuadrat. Jadi, jenis akar dari persamaan kuadrat dapat ditentukan dengan cara mengetahui nilai diskriminan.
Sementara, persamaan kuadrat adalah suatu persamaan yang berbentuk ax2 + bx + c = 0, dengan a, b, dan c sebagai konstanta yang bersesuaian dengan persamaan kuadrat.
Rumus nilai diskriminan persamaan kuadrat ax2 + bx + c = o adalah sebagai berikut.
D = b2 – 4ac
Keterangan:
D = nilai diskriminan
b = koefisien variabel dari x2
a = koefisien variabel dari x
c = konstanta
Pemberian istilah diskriminan D = b2 – 4ac, karena nilai D = b2 – 4ac ini yang telah mendiskriminasikan (membedakan) jenis akar-akar persamaan kuadrat.
Berikut sifat dan fungsi diskriminan pada persamaan kuadrat ax2 + bx + c = 0, dengan a ≠ 0.
- Jika D > 0, maka persamaan kuadrat mempunyai dua akar nyata berlainan (x1 ≠ x2).
- Jika D = 0, maka persamaan kuadrat mempunyai dua akar yang sama, real, dan rasional (x1 = x2)
- Jika D < 0, maka persamaan kuadrat mempunyai akar imajiner atau tidak real.
2. Rumus Diskriminan dan Contoh Soal
Untuk mengetahui akar-akar dari persamaan kuadrat , 
bisa menggunakan rumus ABC.
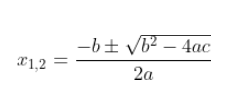
Rumus diskriminan itu ternyata dapat ditemukan dalam rumus ABC. Rumus diskriminan adalah seperti di bawah ini, dengan a, b, dan c sebagai konstanta yang bersesuaian dengan persamaan kuadrat.
D = b² – 4ac
Lalu, rumus ABC dapat juga menjadi seperti ini. Rumus ini dapat dipakai jika yang diketahui adalah nilai diskriminannya.
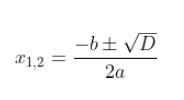
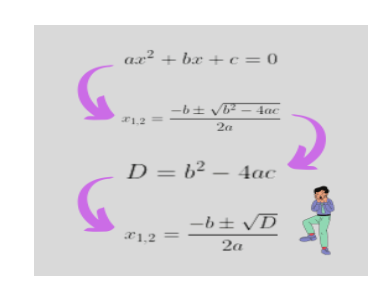
Diskriminan dalam rumus ABC menentukan jenis dari akar-akar persamaan kuadrat berupa bilangan real atau bilangan tidak real. Jenis akar-akar persamaan kuadrat adalah sebagai berikut, guys.
Jika D < 0 atau nilai diskriminan kurang dari 0, maka akar-akarnya adalah tidak real atau imajiner.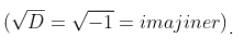 
.
Jika D > 0 atau nilai diskriminan lebih dari 0, maka akar-akarnya adalah real 
dan berbeda atau berlainan 
.
Jika D = 0 atau nilai diskriminan sama dengan, maka akar-akarnya adalah real 
dan sama atau kembar 
.
Berikut beberapa contoh soal diskriminan.
Dari persamaan kuadrat x2 – 10x + 16 = 0, tentukan diskriminan dan jenis akarnya!
Jawab:
x2 – 10x + 16 = 0, berarti a = 1, b = 10, dan c = 16
Nilai diskrimiannya adalah sebagai berikut.
D = b2 – 4ac
= (-10)2 – 4 . 1 . 16
= 100 – 64
= 36
Jadi, nilai diskriminannya adalah 36. Karena D > 0 (36 > 0), maka persamaan kuadrat x2 – 10x + 16 = 0 mempunyai akar-akar rasional.
Contoh Soal 2
Dari persamaan kuadrat x2 + 6x + 9 = 0, tentukan jenis akar persamaan kuadratnya!
Jawab:
x2 + 6x + 9 = 0, berarti a = 1, b = 6, dan c = 9
Nilai diskriminannya adalah sebagai berikut.
D = b2 – 4ac
= (6)2 – 4 . 19
= 36 – 36
= 0
Jadi, nilai diskriminannya adalah 0. Karena D = 0, maka persamaan kuadrat x2 + 6x + 9 = 0 mempunyai akar yang sama.
Demikianlah pembahasan tentang Rumus Diskriminan. Semoga bisa bermanfaat bagi kamu yang sedang membutuhkan informasi penting ini, terima kasih.
