Rumus Kalkulus – Pengertian Kalkulus di ambil dari Kamus Besar Bahasa Indonesia (KBBI) adalah bagian matematika yang melibatkan pengertian dan penggunaan deferensial dan integral fungsi serta konsep yang berkaitan.
Kalkulus dapat diaplikasikan dalam berbagai bidang, seperti sains, teknik, dan ekonomi. Dasar dari kalkulus sendiri adalah membahas konsep limit, turunan (diferensial), dan anti-turunan (integral).
Rumus kalkulus dasar yang meliputi limit, turunan dan integral termasuk dalam ragam rumus matematika.
Kalkulus memiliki beragam penerapan dalam kehidupan sehari-hari. Matematika sebagai salah satu induk ilmu pengetahuan sangat dibutuhkan dalam bidang lain.
Beberapa penerapan kalkulus dalam bidang lain antara lain:
- Pada bidang fisika, khusunya terkait mekanika, kalkulus sangat diperlukan untuk menyelesaikan perhitungan-perhitungan dengan menerapkan konsep kalkulus.
- Dalam bidang statistika dan teori peluang juga terdapat perhitungan dengan menerapkan konsep kalkulus (integral).
- Dalam bidang ekonomi, kalkulus dapat digunakan untuk menentukan biaya marginal (kalkulus diferensial).
Rumus Kalkulus Diferensial
Kalkulus diferensial berkaitan dengan perhitungan turunan fungsi. Turunan merupakan konsep penting dalam kalkulus yang digunakan untuk memahami perubahan nilai suatu fungsi terhadap perubahan variabelnya. Dalam kalkulus diferensial, terdapat beberapa rumus dasar yang perlu dipahami, antara lain:
1. Rumus Turunan Fungsi Dasar
Dalam rumus ini, kita dapat menghitung turunan fungsi dasar seperti konstanta, fungsi linear, fungsi kuadratik, dan lain sebagainya. Contohnya adalah:
f(x) = k (konstanta), f'(x) = 0
f(x) = ax + b (fungsi linear), f'(x) = a
f(x) = ax^2 + bx + c (fungsi kuadratik), f'(x) = 2ax + b
2. Rumus Turunan Fungsi Trigonometri
Rumus ini berguna untuk menghitung turunan fungsi trigonometri seperti sinus, kosinus, dan tangen. Beberapa rumus turunan trigonometri yang penting antara lain:
f(x) = sin(x), f'(x) = cos(x)
f(x) = cos(x), f'(x) = -sin(x)
f(x) = tan(x), f'(x) = sec^2(x)
3. Rumus Turunan Fungsi Eksponensial dan Logaritma
Rumus ini digunakan untuk menghitung turunan fungsi eksponensial dan logaritma. Beberapa rumus turunan yang sering digunakan adalah:
f(x) = e^x, f'(x) = e^x
f(x) = ln(x), f'(x) = 1/x
Turunan dapat disebut juga sebagai diferensial, sementara proses dalam menentukan turunan suatu fungsi disebut sebagai diferensiasi. Menggunakan konsep limit yang sudah dipelajari, umumnya turunan didefinsikan sebagai berikut:

Perbesar
Rumus turunan kalkulus. Foto: Buku Kalkulus Diferensial (Limit, Turunan, dan Aplikasi Turunan) karya Mohammad Rifa’i.
Rumus Turunan pada Kalkulus Diferensial
Berikut rumus-rumus turunan pada kalkulus diferensial, seperti dihimpun dari buku Kalkulus Diferensial (Limit, Turunan, dan Aplikasi Turunan) karya Mohammad Rifa’i:
- f(x) = k f'(x) = 0, ini turunan dari f(x) = c.
- f(x)=x f'(x) = 1, ini turunan dari f(x) = x.
- f(x) = kg(x) f'(x) = kg'(x), ini turunan dari f(x) = ax^n.
- f(x)=x” f'(x) = nx”-1, ini turunan dari h(x) = f(x) + g(x).
- f(x) = u(x) + v(x) f'(x) = u'(x) + v'(x), ini turunan dari h(x) = f(x) – g(x).
- f(x) = u(x). v(x) f'(x) = u'(x) v(x) + u(x) v'(x), ini turunan dari f(x) = u(x) . v(x).
Kalkulus Integral
Kalkulus integral berkaitan dengan perhitungan integral fungsi. Integral merupakan operasi kebalikan dari turunan dan digunakan untuk menghitung luas di bawah kurva fungsi. Berikut adalah beberapa rumus integral yang penting:
1. Rumus Integral Fungsi Dasar
Rumus ini digunakan untuk menghitung integral dari fungsi dasar seperti konstanta, fungsi linear, dan fungsi kuadratik. Contoh rumus integral dasar:
∫(k dx) = kx + C (konstanta)
∫(ax + b dx) = (a/2)x^2 + bx + C (fungsi linear)
∫(ax^2 + bx + c dx) = (a/3)x^3 + (b/2)x^2 + cx + C (fungsi kuadratik)
2. Rumus Integral Fungsi Trigonometri
Rumus ini digunakan untuk menghitung integral dari fungsi trigonometri. Beberapa rumus integral trigonometri yang penting adalah:
∫(sin(x) dx) = -cos(x) + C
∫(cos(x) dx) = sin(x) + C
∫(tan(x) dx) = -ln|cos(x)| + C
3. Rumus Integral Fungsi Eksponensial dan Logaritma
Rumus ini digunakan untuk menghitung integral dari fungsi eksponensial dan logaritma. Beberapa rumus integral yang sering digunakan adalah:
∫(e^x dx) = e^x + C
∫(1/x dx) = ln|x| + C
Integral Tak Tentu
Jika suatu fungsi pangkat diintegralkan, maka akan didapat bentuk umum seperti berikut:
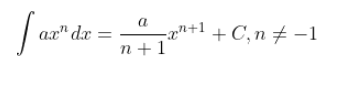
di mana C merupakan bilangan sembarang (konstanta).
Bentuk Pangkat Khusus (n = -1)
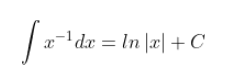
Di mana adalah logaritma natural
Bentuk Khusus
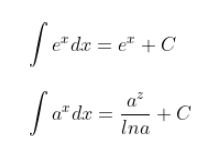
Di mana e merupakan bilangan euler dan a bilangan sembarang positif.
Sifat Integral
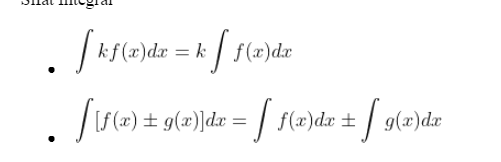
Integral Trigonometri
Bentuk trigonometri juga memiliki integral
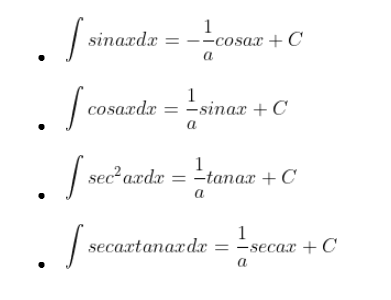
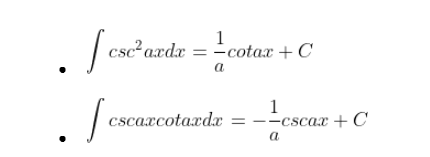
Integral Subtitusi
Integral subtitusi biasanya digunakan pada perkalian dua bentuk fungsi dan salah satunya merupakan turunan dari fungsi lainnya (selisih pangkat tertingginya satu) seperti berikut:
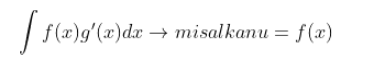
Nah, itulah informasi mengenai Rumus Kalkulus yang bisa kami bagikan. Semoga bermanfaat dan terima kasih telah membaca.




