Contoh Bilangan Kompleks – Bilangan kompleks terdiri dari penjumlahan atau pengurangan bilangan real dan bilangan imajiner yang ditandai dengan notasi j.
Bilangan kompleks = (bilangan real) + j (bagian imajiner)
Sebagai contoh penulisan bilangan kompleks adalah 5 + j3 yang mana angka 5 adalah bagian real sementara 3 adalah bagian imajinernya.
Bilangan kompleks yang dituliskan dengan y = a + bj bisa disingkat dengan pasangan terurut (a, b) sehingga bilangan kompleks juga dapat dituliskan dalam sebuah bidang datar seperti koordinat titik pada sistem koordinat kartesius.
Bidang kompleks atau bidang Argand adalah bidang yang digunakan untuk menggambarkan bilangan kompleks.
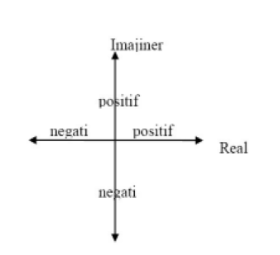
Sehingga apabila terdapat bilangan kompleks y = 4 + 6j, angka 4 adalah bilangan real positif terletak di kuadran I sementara 6 adalah bilangan imajiner positif. Jika dibuat grafiknya akan seperti Gambar 3 di bawah ini.
Seperti halnya koordinat Kartesius, grafik bidang kompleks juga dibagi berdasarkan daerahnya atau kuadrannya. Kuadran pada bidang kompleks dibagi menjadi empat kuadran berdasarkan letak posisi sudutnya.
- Kuadran I ada pada sudut 0 sampai dengan 90⁰
- Kuadran II ada pada sudut 90⁰ sampai dengan 180⁰
- Kuadran III ada pada sudut 180⁰ sampai dengan 270⁰
- Kuadran IV ada pada sudut 270⁰ sampai dengan 360⁰
Contoh Bilangan Imajiner
Dalam bidang matematika aljabar, pengertian bilangan imajiner adalah bilangan yang dapat didefinisikan dengan i² = -1, dengan i merupakan simbol angka imajiner. Bilangan i dalam bahasa inggris disebut juga imaginary number. Nilai imajiner sering digunakan dalam ilmu teknik elektro dan fisika.
Nilai bilangan imajiner dapat diperoleh melalui persamaan kuadratik berikut.
x² + 1 = 0
x² = -1
x = √-1
Secara numerik tidak ada nilai x, yang memenuhi nilai √-1. Sehingga digunakan simbol i untuk mendefinisikan nilai tersebut.
diperoleh
x = √-1 = i
berlaku
i2 = i × i
= √-1 × √-1
= -1
jadi, nilai imajiner didefinisikan sebagai
i2 = -1
Bilangan imajiner merupakan bagian dari bilangan kompleks, berikut 10 contoh bilangan imajiner. Bilangan imajiner merupakan suatu simbol sehingga pada dasarnya tidak ada dan hanya dituliskan saja sebagai bahasa komputasi. Berikut beberapa contoh bilangan imajiner pada operasi aljabar.
- Penjumlahan
Operasi penjumlahan pada bilangan imajiner secara umum sama saja dengan operasi biasa. Karena selalu merupakan bilangan kompleks, maka untuk dapat menghitungnya, harus dikelompokkan terlebih dahulu antara bilangan riil dan imajiner. Misalnya seperti yang terlihat pada contoh di bawah ini.
- (7 + 2i) + (8 + 3i)
maka penyelesaiannya:
= (7 + 8) + (2i + 3i)
= 15 + 5i
Jadi, hasil dari (7 + 2i) + (8 + 3i) adalah 15 + 5i
Contoh lainnya misalkan:
- (13 + 8i) + (3-6i)
maka penyelesaiannya:
= (13 + 3) + (8i – 6i)
= 16 + 2i
Jadi, hasil dari (13 + 8i) + (3-6i) adalah 16 + 2i
- Pengurangan
Pada operasi pengurangan, cara perhitungannya hampir sama dengan penjumlahan. Bilangan riil dikelompokkan sendiri, begitu pula imajiner. Kemudian, baru dilakukan pengurangan. Misalnya seperti contoh yang diberikan di bawah ini:
- (3 + 3i) – (2 – 9i)
maka penyelesaiannya:
= (3 – 2) + (3i – (-9i))
= 1 + 12i
Jadi, hasil dari (3 + 3i) – (2 – 9i) adalah 1 + 12i
Contoh yang lainnya adalah:
- (9 – 2i) – (7 – 8i)
maka penyelesaiannya:
= (9 – 7) + (-2i – (-8i))
= 2 + 6i
Jadi, hasil dari (9 – 2i) – (7 – 8i) adalah 2 + 6i
Kesimpulannya, bahwa bilangan imajiner ini tidak nyata, tetapi penting keberadaannya pada disiplin ilmu yang lainnya, terutama fisika, karena setiap arus yang masuk maupun keluar dinyatakan dengan nilai i.
Contoh Soal Bilangan Kompleks
Berikut ini contoh soal bilangan kompleks.
- Soal 1
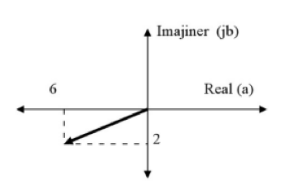
Buatlah ke dalam bentuk grafik dari bilangan kompleks y = -6 – j2
Jawab:
Angka -6 adalah bilangan real negatif sementara -2 adalah bilangan imajiner negatif sehingga terletak di kuadran III. Jika dibuat grafiknya akan seperti gambar di bawah ini.
- Soal 2
Tentukan berapa hasil penjumlahan dan pengurangan dari bilangan di bawah ini
x1 = 5 + j4 dan x2 = 2 – j3
a. x1 + x2
b. x1 – x2
Jawab:
a. x1 + x2
= (5 + j4) + (2 – j3)
= (5 + 2) + j (4 – 3)
= 7 + j (j1 bisa dituliskan dengan notasi j saja)
b. x1 – x2
= (5 + j4) – (2 – j3)
= (5 – 2) + j (4 + 3)
= 3 + j7
Itulah beberapa contoh bilangan kompleks beserta materinya yang bisa kamu jadikan panduan ketika memahami materi ini. Semoga bisa membantu dan terima kasih.




