Persamaan Garis Singgung Lingkaran – Persamaan garis singgung merupakan persamaan garis yang menyinggung lingkaran di satu titik. Suatu garis disebut garis singgung jika memiliki tepat satu titik persekutuan atau titik potong terhadap lingkaran atau kurva.
Lalu, apa perbedaan garis singgung lingkaran dan kurva? Perbedaannya terletak pada objek yang disinggung. Jika suatu garis menyinggung lingkaran, maka garis singgungnya disebut garis singgung lingkaran.
Sebaliknya, jika yang di singgung berupa kurva, maka garis singgungnya disebut garis singgung kurva.
Persamaan Garis Singgung Lingkaran dengan Gradien
Sebagaimana telah kita pelajari bahwa persamaan lingkaran yang berpusat di O(0,0) adalah \( x^2 + y^2 = r^2 \). Persamaan garis singgung terhadap lingkaran \( x^2 + y^2 = r^2 \) dengan gradien \(m\) dapat ditentukan sebagai berikut:
- Misalkan persamaan garis dengan gradien \(m\) adalah \( y = mx + n \)
- Substitusikan \( y = mx + n \) ke persamaan lingkaran \( x^2 + y^2 = r^2 \), sehingga diperoleh
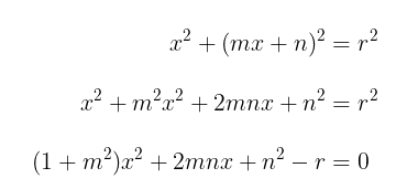
Dapat Anda lihat bahwa persamaan ini adalah suatu persamaan kuadrat dengan variabel x. Garis menyinggung lingkaran, artinya diskriman dari persamaan kuadrat tersebut sama dengan nol (persamaan kuadrat mempunyai akar kembar).
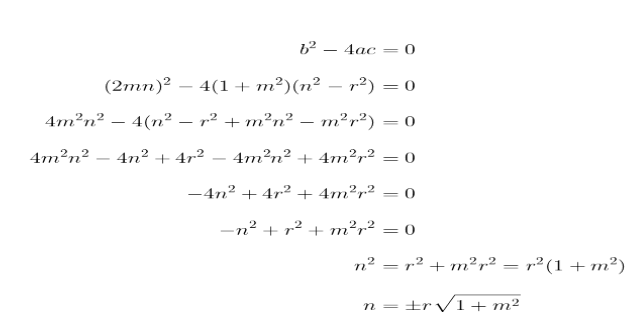
Setelah itu, \(n\) disubstitusikan ke dalam persamaan garis \( y = mx + n \).
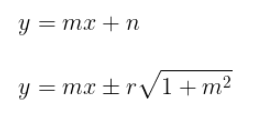
Jadi, persamaan garis singgung dengan gradien \(m\) terhadap lingkaran \( x^2 + y^2 = r^2 \) adalah
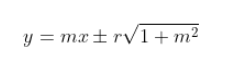
Persamaan Garis Singgung Lingkaran Dengan Gradien m
Persamaan lingkaran dengan puat (0,0) adalah x2 + y2 = R2
Garis singgung pada lingkaran ini adalah
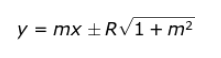
Persamaan lingkaran dengan puat (0,0) adalah (x — a)2 + (y — b)2 = R2
Garis singgung pada lingkaran ini adalah
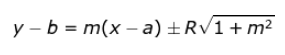
Jika lingkaran berupa bentuk umum x2 + y2 + Ax + By + C= 0 maka garis singgungnya adalah
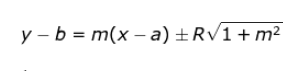
dengan
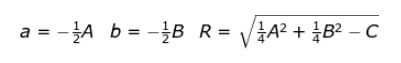
Contoh Soal 1 :
Persamaan garis singgung lingkaran x2 + y2 = 180 dengan gradien 2 adalah …..
Jawab :
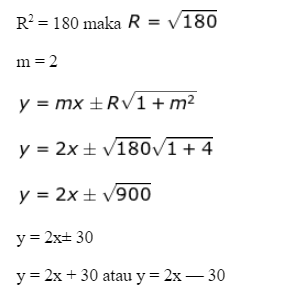
Contoh Soal 2 :
Tentukan persamaan garis singgung lingkaran (x — 4)2 + (y + 2)2 = 250 yang bergradien 3 adalah …..
Jawab :
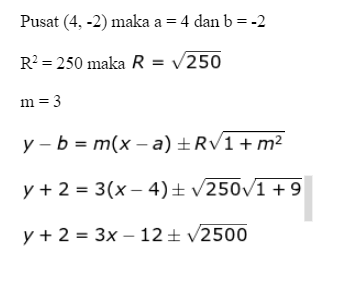
y + 2 = 3x — 12 ± 50
y = 3x — 14 ± 50
y = 3x — 14 + 50 atau y = 3x — 14 — 50
y = 3x + 36 atau y = 3x — 64
Contoh Soal 3 :
Tentukan persamaan garis singgung lingkaran x2 + y2 — 4x + 6y — 55 = 0 yang bergradien 4 adalah …..
Jawab :
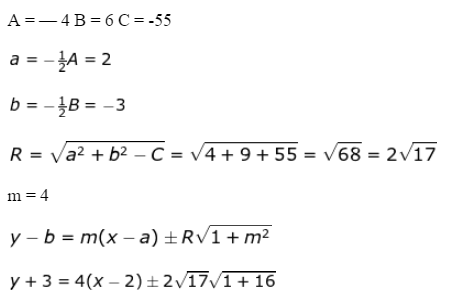
y + 3 = 4x — 8 ± 34
y = 4x — 11 ± 34
y = 4x — 11 + 34 atau y = 4x — 11 – 34
y = 4x + 23 atau y = 4x — 45
Nah, itulah informasi mengenai Persamaan Garis Singgung Lingkaran. Semoga informasi yang kami bagikan ini bermanfaat dan terima kasih telah membaca.







